Zielorientierte Adaptivität für nichtlineare Homogenisierungen mittels hierarchischer Modelle

Enlarge image

Zusammenfassung

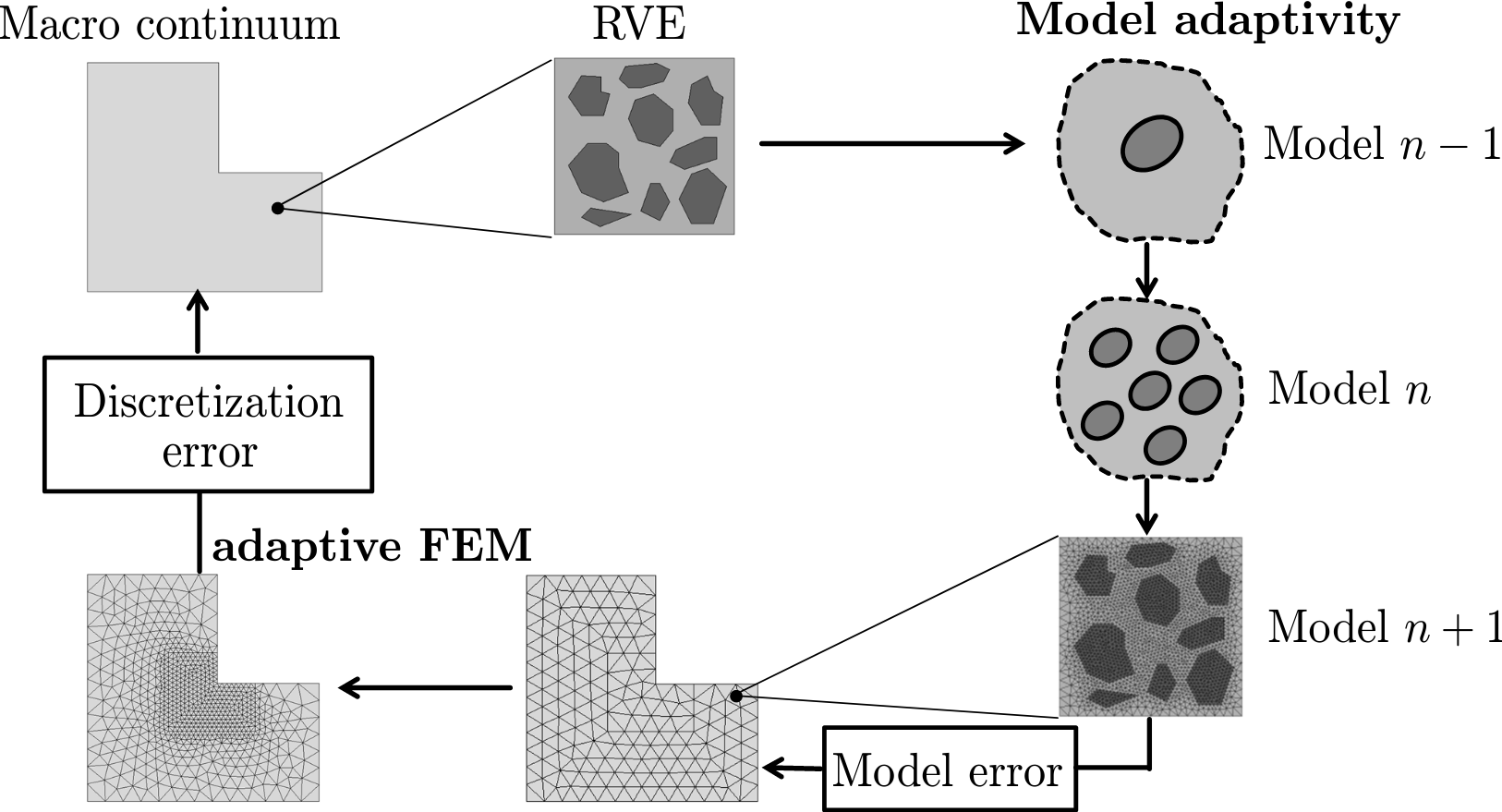
Die Entwicklung und Herstellung innovativer Produkte unter Verwendung neuartiger Materialien erfordert fundierte Kenntnisse der Simulationsmethoden für eine sichere Auslegung von Bauteilen und Maschinen. Die zunehmende Verwendung heterogener Materialien wie Verbundwerkstoffe in der industriellen Praxis hat die Finite-Elemente-Simulation in Kombination mit der Homogenisierungstechnik zu einem weit akzeptierten und häufig sogar unvermeidlichen Werkzeug gemacht. Ein Bauteil wird häufig auf der Makroebene ausgelegt, welches mit Hilfe von Standard-Finite-Elemente-Methoden (FEM) simuliert werden kann, deren (räumlichen) Diskretisierungsfehler durch eine adaptive Netzverfeinerung leicht kontrollierbar sind. Viel komplizierter wird es, wenn das Material auf einer bestimmten Längenskala (z.B. mikro) inhärente Heterogenitäten aufweist. Man muss sich mit diesen Heterogenitäten auf dieser Skala auseinandersetzen und dann einen Skalenübergang durchführen, um das effektive Verhalten auf der Makroskala zu erhalten (oft als Homogenisierung bezeichnet). Es wurden beträchtliche Anstrengungen unternommen, um die mit der Homogenisierung verbundenen Rechenkosten zu verringern, die häufig als Homogenisierung reduzierter Ordnung angesehen werden. Der resultierende Modellfehler bleibt jedoch in der Regel unkontrolliert. Dieses Projekt befasst sich mit der numerischen Effizienz nichtlinearer Homogenisierungsprobleme durch eine selektive Verwendung zeitaufwändiger und genauer Homogenisierungsmethoden nur auf lokalen Makrodomänen, wo dies erforderlich ist. Zu diesem Zweck wird die Modelladaptivität als vielversprechende Methode für Plastizitätsprobleme entwickelt. Ähnlich wie bei der adaptiven FEM beginnt sie mit einer effizienten Homogenisierungsmethode, und dann wird durch eine Schleifenfehlerkontrolle ein lokaler Wechsel zu genauen Homogenisierungsmethoden durchgeführt, um die Genauigkeit zu verbessern (als Modellverfeinerung bezeichnet). Wie hierarchische FE-Strukturen für adaptive FEM müssen hierarchische Modelle für die Modelladaptivität erstellt werden. Wir werden eine Vielzahl von nichtlinearen Homogenisierungsmethoden abdecken und dabei Mean-Field-, Modellreduktions- und numerische Methoden berücksichtigen. Sowohl Nichtlinearitäten als auch die Zeitabhängigkeit des Plastizitätsproblems werfen einige Schwierigkeiten für die Fehlerschätzung auf, die in diesem Projekt behandelt werden. Um eine vollständige Fehlerkontrolle zu erreichen, wird die Modelladaptivität mit adaptiven Finite-Elementen in Raum und Zeit gekoppelt.

 

abstract

The development and the production of innovative products using novel materials require in-depth knowledge of simulation methods for a safe design of components and machines. The increasing use of heterogeneous materials like composites in the industrial praxis has made the finite element (FE) simulation using homogenization techniques a well-accepted and often even inevitable tool. A machine component is designed to serve on a macro level, which may be simulated by means of standard finite element methods (FEM), whose (spatial) discretization errors can be easily controlled by an adaptive mesh refinement. It becomes much more complicated, when the material possesses inherent heterogeneities on a certain length scale (say micro).  One has to deal with these heterogeneities on that scale and then perform scale transition to obtain the overall behavior on the macro scale, which is often referred to as homogenization. Considerable effort has been paid to reduce the computational cost associated with homogenization, often regarded as reduced order homogenization. However, the resulting model error is usually left uncontrolled. This project deals with the numerical efficiency of nonlinear homogenization problems with a selective use of time-consuming, accurate homogenization methods only on local macro domains where needed. To this end, model adaptivity, as a promising methodology, will be developed for plasticity problems. Quite similarly to the adaptive FEM, it starts with an affordable homogenization method, and then through a loopwise error control, a local switch to accurate homogenization methods is performed to enhance the accuracy (referred to as model refinement). Like hierarchical FE structures for adaptive FEM, hierarchical models need to be established for model adaptivity. Covering a large variety of nonlinear homogenization methods, we will consider mean-field, model order reduction and computational methods. Both nonlinearities and time-dependency of the plasticity problem rise some difficulties for error estimate to be addressed in this project. Towards a full error control, model adaptivity will be coupled to adaptive space-time finite elements.

 

Veröffentlichungen

Förderinstitutionen

DFG, GZ: MA 1979/30-2