Adaptive Finite-Elemente-Methoden zur Parameteridentifikation von hierarchischen Modellen für Elastomere
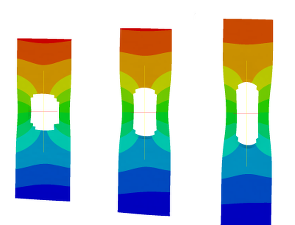
Die Identifikation von Materialparametern für konstitutive Materialmodelle für Polymere unter Berücksichtigung von inhomogenen Spannungs- und Dehnungszuständen soll mittels der Minimierung eines Kleinste-Quadrate Funktionals erfolgen.
Die dafür nötigen experimentellen Daten werden typischerweise mit Hilfe von optischen Meßsystemen gewonnen. In jedem Iterationsschritt dieses Minimierungsproblems wird eine volständige FE-Rechnung durchgeführt, was für einen verhältnismäßig hohen Rechenaufwand sorgt. Es ist daher erstrebenswert, eine effiziente Diskretisierung zu finden, um den Aufwand möglichst gering zu halten.
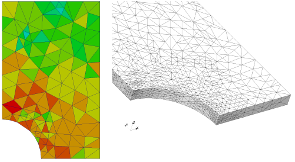
Der LTM geht dieses Problem an, indem das FE-Netz adaptiv verfeinert wird. Grundlage dieser Verfeinerung sind a-posteriori Fehlerindikatoren [2], die zu zielgerichtet verfeinerten Netzen führen. Die Fehlerindikatoren werden für stabilisierte Dreiecks- und Tetraeder-Elemente mit niedriger Ansatzordnung entwickelt. Diese Elemente eigen sich besonders für die Vernetzung von komplizierten Geometrien als auch für Netzverfeinerungen. Außerdem können durch die Verwendung einer gemischten Verschiebungs-Druck Formulierung Locking-Effekte bei (nahezu) inkompressiblem Materialverhalten vermieden werden und dabei auftretende Spannungsoszillationen reduziert werden [1,3]. Die Behandlung dieser Stabilisierungsterme im Rahmen der Fehlerindikatoren sind ebenfalls Gegenstand aktueller Forschung.
Literatur
- K.-U. Widany, I. Caylak, R. Mahnken: Stabilized Mixed Tetrahedrals with Volume and Area bubble functions at Large Deformations, PAMM, 10, 227-228 (2010).
- R. Becker, B. Vexler: A posteriori estimation for finite element discretization of parameter identification problems, Numer. Math., 96, 435-459 (2004).
- R. Mahnken, I. Caylak: Stabilization of bi-linear mixed finite elements for tetrahedra with enhanced interpolation using volume and area bubble functions, Int. J. Numer. Meth. Engng, 75, 377-413 (2008).
Förderinstitution:
Deutsche Forschungsgemeinschaft DFG, GZ: MA 1979/10-1
Veröffentlichungen:
- K.-U. Widany, I. Caylak und R. Mahnken. „Stabilized Mixed Tetrahedrals with Volume and Area Bubble Functions at Large Deformations“. Proc. Appl. Math. Mech. Bd. 10. 2010, S. 227–228. doi: 10.1002/pamm.201010106
- K.-U. Widany und R. Mahnken. „Approximation of the dual problem for error estimation in inelastic problems“. Proc. Appl. Math. Mech. Bd. 14. 2014, S. 273– 274. doi: 10.1002/pamm.201410124
- K.-U. Widany und R. Mahnken. „An error indicator for parameter identificationwith stabilized mixed tetrahedrals“. Proc. Appl. Math. Mech. Bd. 11. 2011, S. 229–300. doi: 10.1002/pamm.201110141
- I. Caylak, R. Mahnken und K.-U. Widany. „Stabilized mixed triangular finite elements at large deformations using area bubble functions“. Proc. Appl. Math. Mech. Bd. 11. 2011, S. 201–202. doi:10.1002/pamm.201110092
- K.-U. Widany und R. Mahnken. „Adaptivity for parameter identification of incompressible hyperelastic materials using stabilized tetrahedral elements“. Comput. Methods Appl. Mech. Engrg. 245-246 (2012), S. 117–131. doi: 10.1016/j.cma.2012.06.017
- K.-U. Widany und R. Mahnken. „Adaptive FEM with Stabilized Elements for Parameter Identification of Incompressible Hyperelastic Materials“. Proc. Appl. Math. Mech. Bd. 12. 2012, S. 213–214. doi: 10.1002/pamm.201210097