Fuzzy Finite Elemente Methode für hybride Systeme

In vielen FE-Anwendungen herrschen häufig unterschiedliche Arten von Unsicherheiten bezüglich der Materialparameter des Simulationsmodells. Diese Unsicherheiten entstehen durch ungenaue, linguistische, unvollständige oder statistische Eigenschaften.

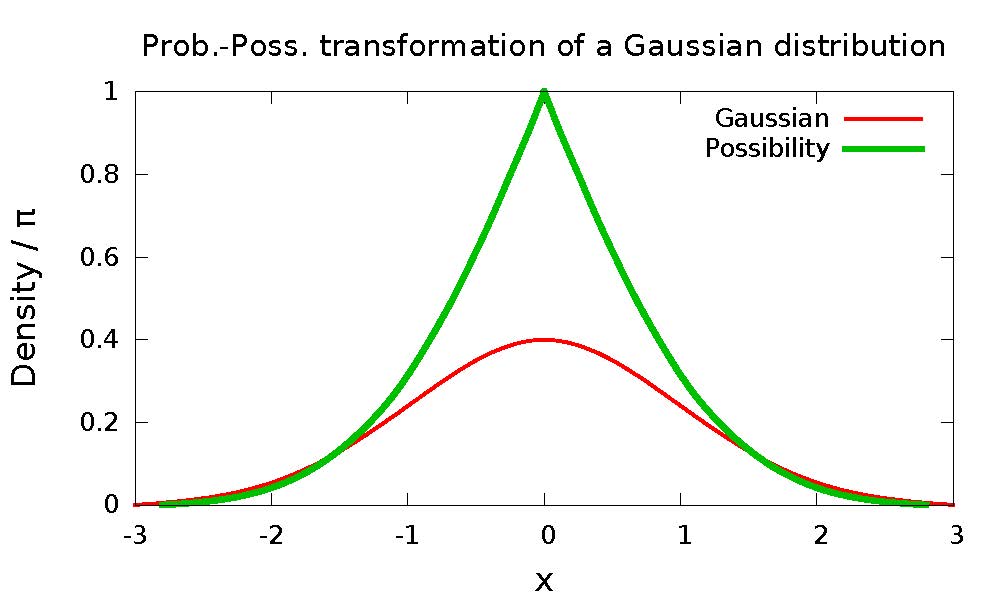
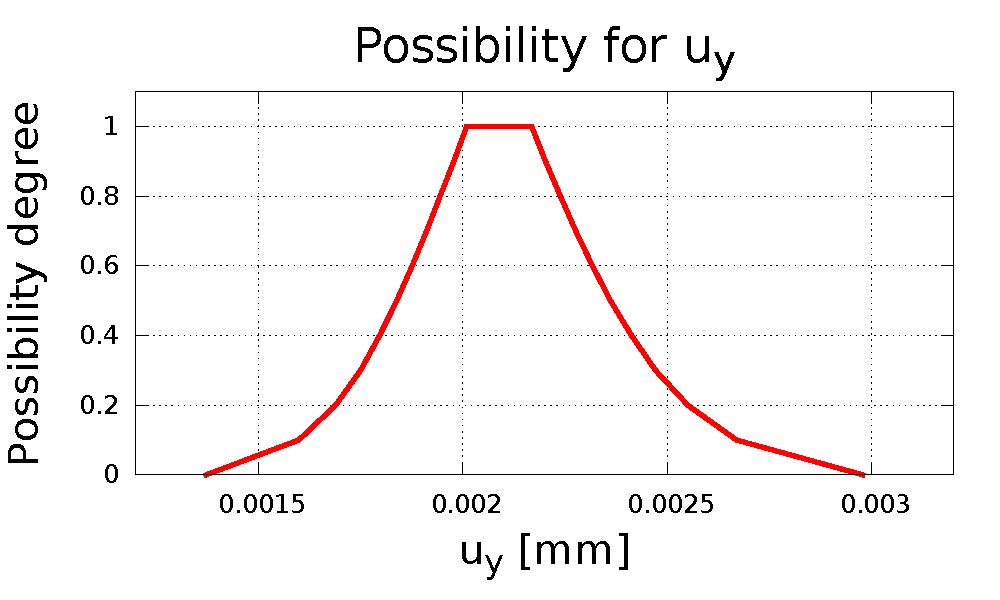
Hieraus ergeben sich Unsicherheiten in der Systemantwort und somit in der numerischen Simulation. Während die stochastische Methode eine Möglichkeit zur Quantifizierung der statistischen Unsicherheiten erlaubt, benötigen die weiteren Arten der Unsicherheit eine Fuzzy Methode. Hierbei beschreiben Fuzzy Zahlen bzw. Possibilitätsverteilungen die unsicheren Systemparameter. Dies bedeutet, dass die allgemeine Lösung für ein mechanisches Randwertproblem mit einer Fuzzy Finite-Element-Methode (FFEM) erfolgt.

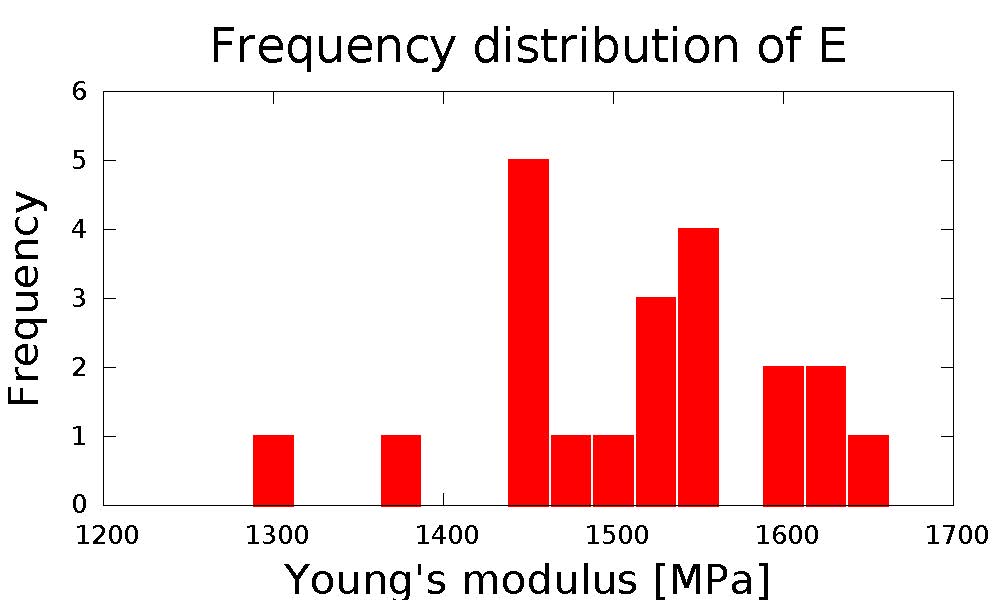
Bei hybriden Strukturen handelt es sich um einen Verbund von z.B. Metallen und Prepregs (preimpregnated fibres). Für Metalle ist die Anzahl der Einflussgrößen für Unsicherheiten in Folge der Herstellung überschaubar. Bei den Prepregs gibt es hingegen mehrere Einflussgrößen, die einer Verteilung bzw. Unschärfe unterliegen. Die Wichtigsten sind die Ingenieurkonstanten, die Aushärtung der Matrix, die Ausrichtung der Fasern und die Volumenanteile der Fasern. Bei der Kombination zu einem Hybridbauteil haben dann weitere Faktoren, wie z.B. die Verbindung der einzelnen Komponenten oder auch unterschiedliche Wärmeausdehnungskoeffizienten einen Einfluss. Die finalen Eigenschaften des Verbundes können aufgrund der Fülle von Randparametern daher nur schwer durch experimentelle Daten sicher bestimmt werden. Das wesentliche Ziel ist daher die Erfassung der Unschärfe, welche zusätzlich zur stochastischen Unsicherheit existieren kann, und ihre Berücksichtigung in der FE-Simulation.